Spatial Transformer Networks
如何在网络内部对局部数据实施主动空间变换

封面图片: Milad B. Fakurian
面试的时候被问到了这个网络,所以这里补下课。Spacial Transformer Network 是由来自DeepMind的Max Jaderberg等人在2015年发表的文章,描述了一种可以嵌入到卷积神经网络中实现特定区域的提取与仿射变换的结构模块。你可以在这里找到原文。

本文是与之相关的学习笔记。
卷积神经网络已经在不同的领域大放光彩,但是作者认为一个良好的系统在识别物体姿态与部分形变时应当不受纹理与形状的影响。CNN的局部最大池化在某种程度上可以摆脱这种影响,但是由于池化尺度较小,只有在网络层数较深时才能实现。CNN内部的特征图依旧会受输入图像众较大变换的影响。这种受限的预定义池化机制限制了CNN处理空间尺度分布数据的能力。
为解决此问题作者提出了Spacial Transformer的概念。它可以嵌入到标准的神经网络架构中并提供空间变换能力。这种变换是基于样本的,并且是在训练过程中习得的。与池化的固定感受野不同,这种变换是动态的,而且因输入不同而不同。同时变换也是全局的,可以提供缩放、裁切、旋转以及其它非刚性变换。这使得网络不经可以选择图像中相关性最大的区域,还可以将这个区域变换到更加合适的状态,降低后续的处理难度。Spacial Transformer是可微的,这意味着可以嵌入到神经网络并使用反向传播优化。
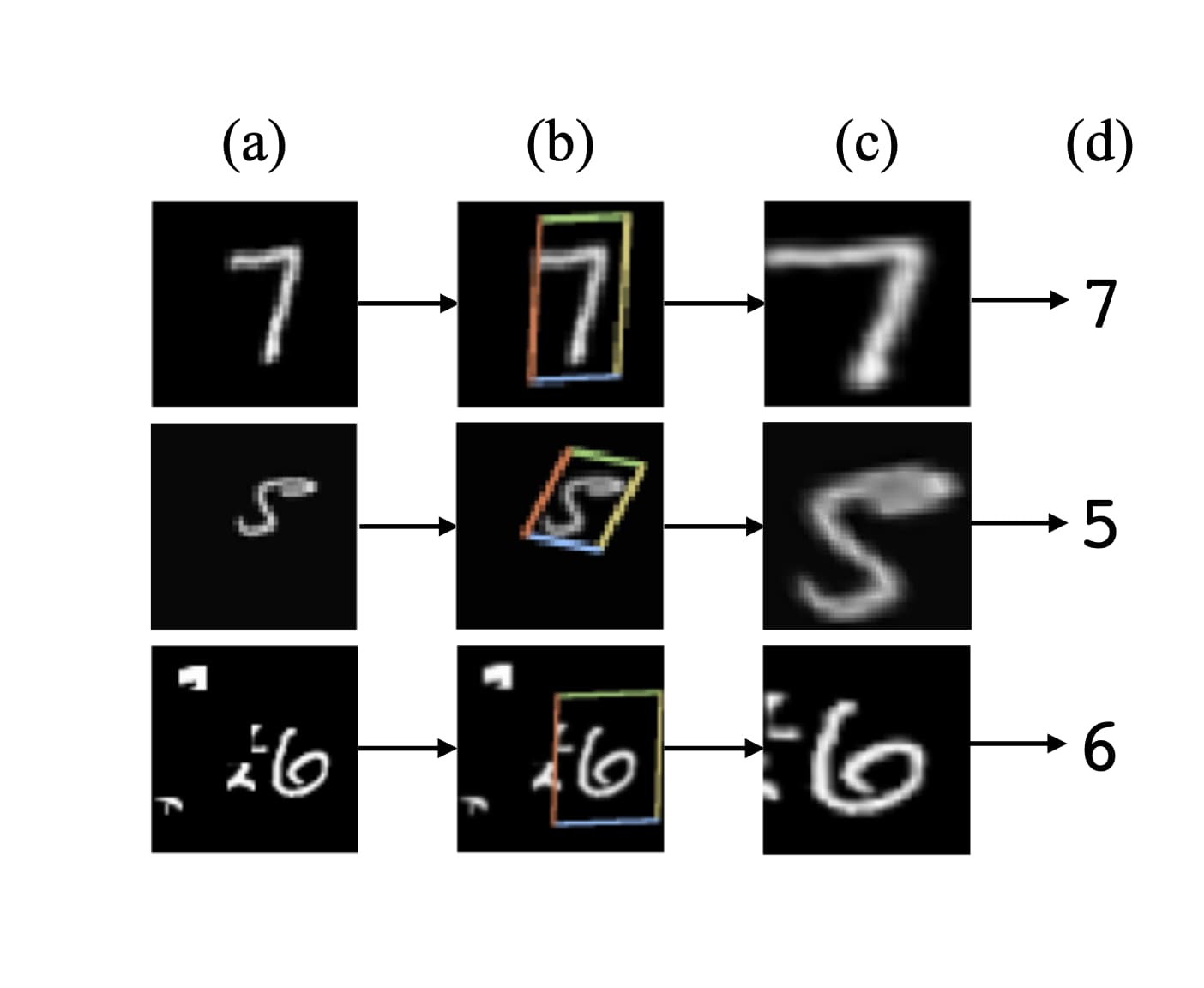
Spatial Transformer可以用在多种图像任务中,例如(1)图像分类。例如MNIST数字图像识别,但是图像中的数字区域是非标准的,会有偏移、旋转、杂质等状况。(2)协同定位。给定同类物体的多个图像,Spatial Transformer可以在图像中定位这些物体。(3)空间注意力。Spatial Transormer可以用在需要注意力机制的任务中,并且不需要强化学习。使用注意力机制的好处在于可以将变换后的低分辨率输入与原始高分辨输入结合,提升计算效率。
Spatial Transformer
Spatial Transformer是一种可以在单次前向传播时对单个特征图实施空间变换并输出新特征图的可微模块。变换的形式取决于具体的输入内容。对于多通道输入,变换在每个通道上分别执行。
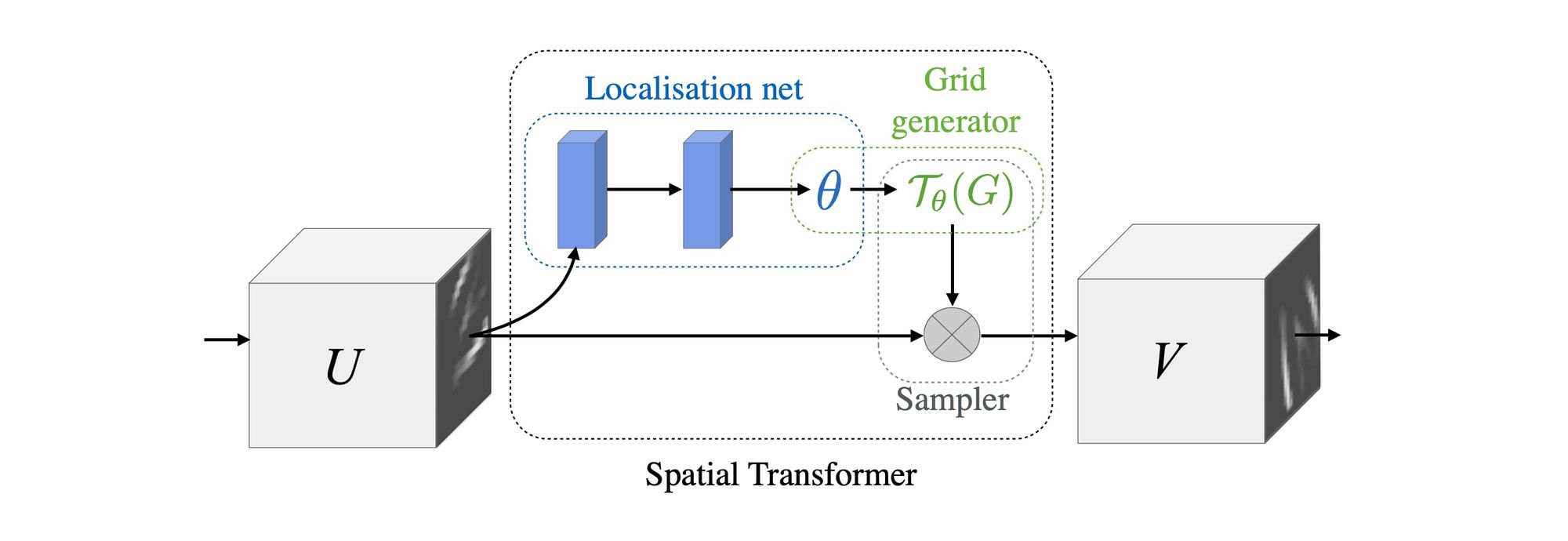
Spatial Transformer机制包含三个部分。首先由定位网络(Localisation Network)接收输入特征图,然后输出空间变换所需的参数;之后由网格生成器(Grid Generator)依据该参数生成采样网格,并用在输入特征图上;最后,采样器(sampler)根据特征图与采样网格,输出采样变换后的特征图。
定位网络
定位网络的输入为特征图,输出为参数 θ。视将来要实施的变换种类,θ 的取值可变。例如典型的仿射变换包含6个参数。定位网络的形式不限,可以是卷积网络也可以是全连接,只要最后输出变换参数即可。
参数化的采样网格
一张特征图经过采样网格处理之后会生成新的特征图,其大小则取决于采样网格的分辨率,通道数则与输入特征图的通道数相同。与采样网格匹配的变换是参数化的,例如仿射变换就可以使用6个参数来定义:
$$\begin{pmatrix} x_i^s\\y_i^s\end{pmatrix} = \begin{bmatrix} \theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22}& \theta_{23} \end{bmatrix} \begin{pmatrix} x_i^t\\y_i^t \\ 1 \end{pmatrix}$$
其中$x_i^t, y_i^t$是输出特征图网格坐标,$x_i^s, y_i^s$是网格对应的输入特征图的坐标,取值范围归一化。改变网格的参数即可获得下图(b)中所展示的局部提取效果。
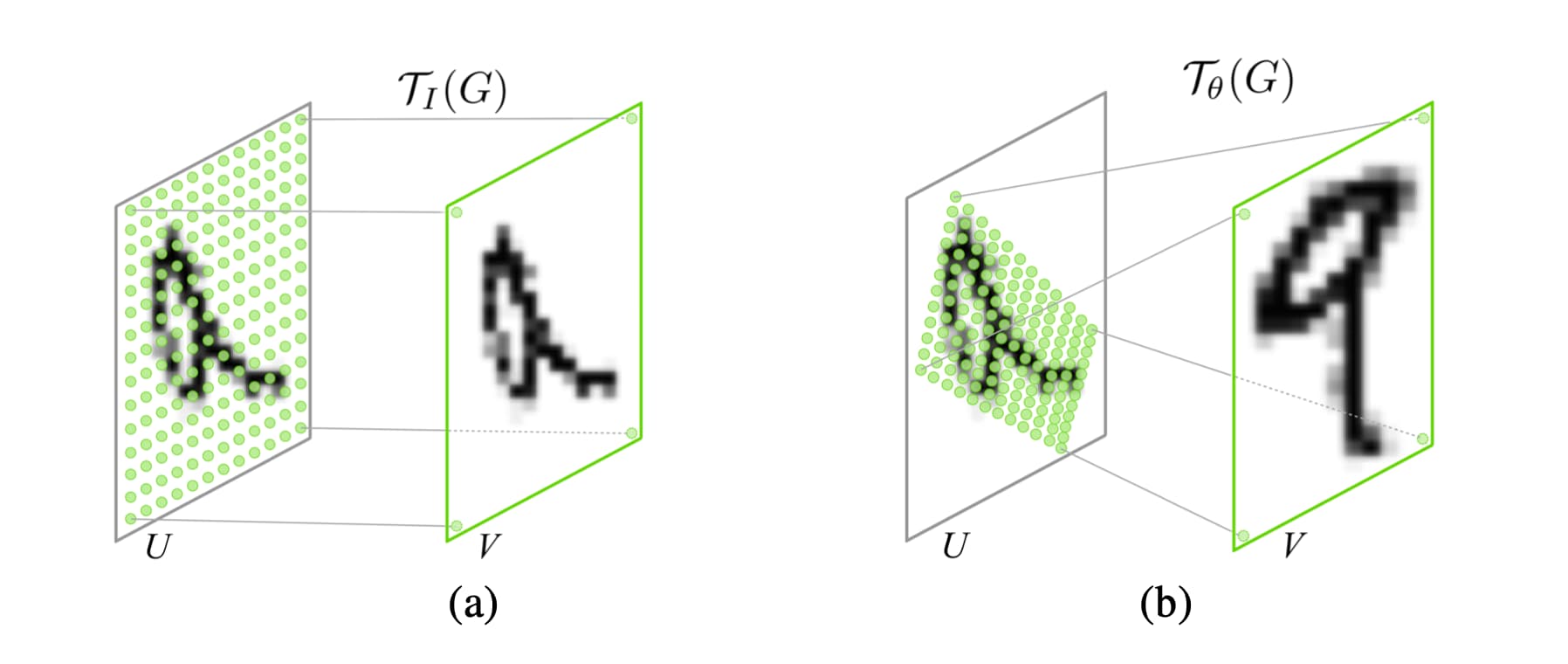
实际上,这种变换可以写作一般形式:
$$\tau_\theta = M_\theta B$$
其中B为网格、M为参数矩阵。这两个参数是可以通过反向传播更新的。
可微的图像采样
图像采样过程可以写为:
$$V_i^c=\sum_n^H\sum_m^WU_{nm}^ck(x_i^s-m;\Phi_x)k(y_i^s-n;\Phi_y) \forall{i}\in[1...H'W'] \forall{c}\in[1...C]$$
其中$\Phi_x, \Phi_y$是采样核(kernel)的参数,决定了具体的采样方式。
$U_{nm}^c$为输入特征图通道$c$在位置$(n, m)$处的数值。$V_i^c$为对应的输出特征图通道$c$在位置$i$的数值。这个式子中,V对U、V对x、y均是可微的,所以可以使用反向传播来更新参数。
Spatial Transformer Networks
定位网络、采样网格与采样器结合起来就是。它可以作为一个模组以任意数量嵌入到卷积神经网络中,构成Spatial Transformer Networks。将Spatial Transormer嵌入到卷积神经网络中会迫使网络学习如何主动变换输入特征图以从全局降低loss。而具体的变换方式则存储在定位网络以及之前的神经网络权重参数中。在某些任务中定位网络输出的参数$\theta$也可以继续向前传播,毕竟它包含了有用信息。
通过指定网格的宽度与高度参数,Spatial Transformer还可以用来降采样或者升采样特征图。不过由于采样核支持的尺寸有限,降采样可能会带来锯齿效应。
你可以在一个神经网络的不同深度层使用Spatial Transformer,也可以将它们并行起来从特征图中提取多个物体,不过这样会限制模型能够识别的区域数量。
实验
作者开展了一系列实验来证明Spatial Transformer的有效性。
第一个为扭曲的MNIST数据集。具体的扭曲手段包括旋转、缩放、平移、透视与弹性扭曲。作者将Spatial Transformer置于网络的最前端,采样方法均为双线性插值,变换方式则包括仿射变换、透视变换与16点thin plate spline transformation。训练后发现使用Spatial Transformer之后的效果要优于没有使用的效果,并且thin plate spline transformation的效果最好。

这里还有作者上传的一段视频,展示了更多变换过程细节。
第二个实验为门牌号识别。
这个实验中放置了多个Spatial Transformer。第一个在网络最前端,定位网络为一个4层卷积网络。之后每隔4个卷积层放置一个Spatial Transformer,但是它们的定位网络为两层包含32个单元的全连接层。所有的Spatial Transformer使用双线性插值与仿射变换。
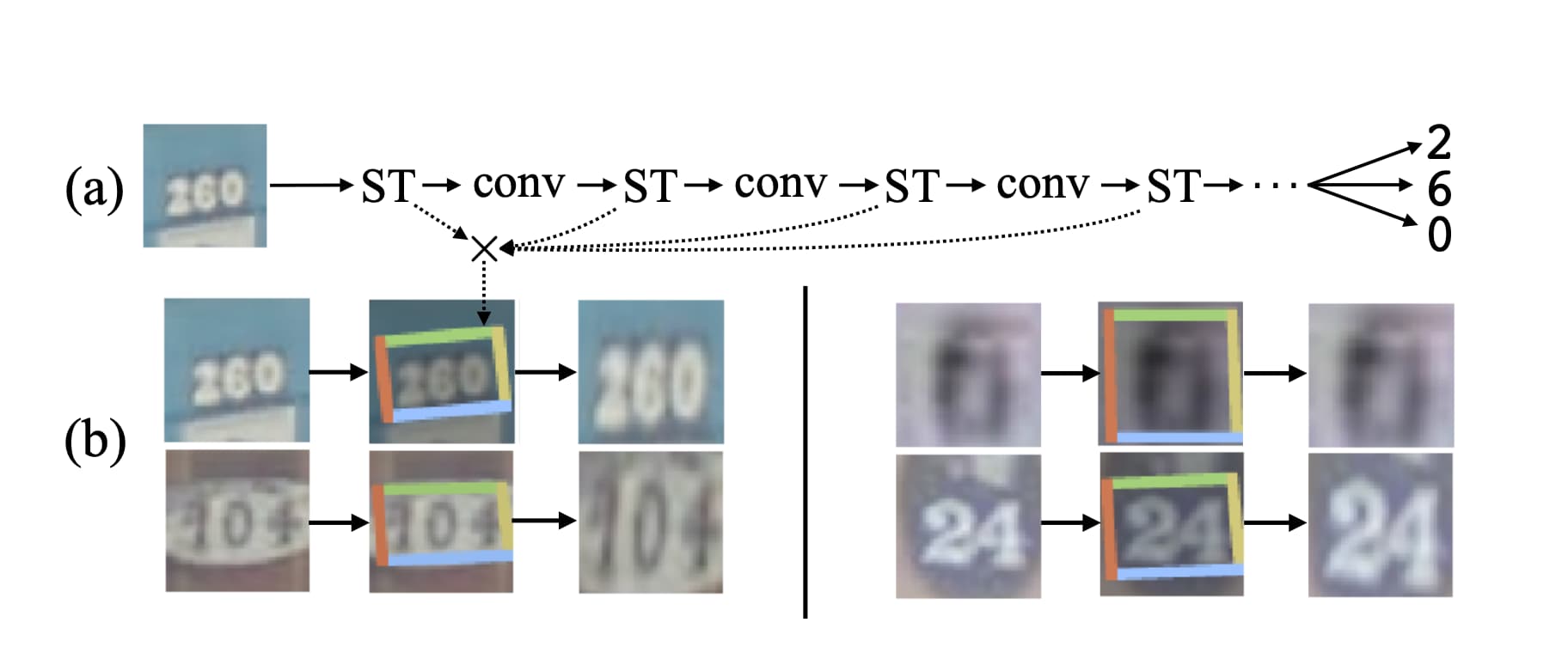
实验结果显示Spatial Transformer可以降低错误率并获得SOTA的结果。
第三个实验为细粒度分类。实验中模型要对鸟类的具体类别做出判断。这个实验中的Spatial Transformer分布在网络的前端且呈现并行排布,它们输出的图像则馈入到多个子网络中,并将最终的特征图拼接在一起实现分类。
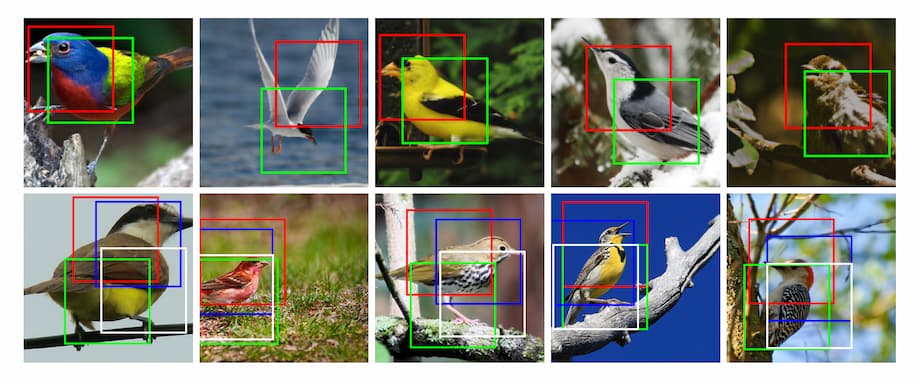
这个过程中,不同的Spatial Transformer学习到了不同的特征区域。例如上方图像中红色的Spatial Transformer对于鸟类的头部区域情有独钟。最终的识别准确率比之前的最佳结果提升了1.2个百分点。
总结
Spatial Transformer可以看做是一个可以嵌入到卷积神经网络中的具备主动空间变换功能的特殊结构。它是可学习的,并且不需要额外的标签。在一些特殊的应用中可以考虑使用。
另外,Google的Attention Mesh就使用了Spatial Transformation来实现面部特定区域的特征点检测。具体可以参考:







Comments ()