残差网络解决了什么问题

残差网络（Residual Networks）是由微软亚洲研究院的Kaiming He等人提出的神经网络模型。依托该模型，他们获得ILSVRC & COCO 2015图像分类竞赛第一名。你可以在这里找到论文正文：

Deep Residual Learning for Image Recognition

Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously. We explicitly reformulate the layers as learning residual functions with reference to the layer inputs, instead of l…

arXiv.orgKaiming He

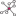
这篇文章非常经典，推荐精读。以下是对该论文核心内容的摘抄。

网络退化

神经网络的深度已然被认为是影响网络表现的一个核心因素。但是极深网络的训练面临着梯度消失与爆炸的干扰。归一化（normalization）的引入很大程度上解决了这个问题，使得数十层深的网络得以收敛。但是新的问题又浮现了出来，网络开始退化——随着深度增加，准确率趋于饱和，之后迅速衰退。这并非由过拟合（overfitting）造成，并且给已经很深的模型增加更多的层数会导致更高的训练误差。

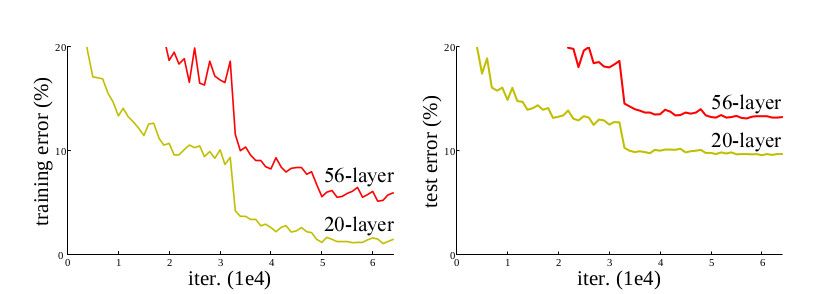
学习残差

为了解决这一问题，作者提出了深度残差学习（deep residual learning）的概念：堆叠的网络需要拟合的不再是设想中的隐含映射，而是全新的残差映射。如果将设想中的隐含映射记为

$$ H(x) $$

则残差映射可以表示为

$$ H(x) + x $$

作者认为这种全新的映射拟合起来更加容易。例如拟合恒等映射时，相比堆叠多个非线性层来拟合，将残差置0显然更加简单。

快捷连接

如果将残差连接记为$F(x)$，由上一公式可得

$$ F(X) = H(x) - x $$

将$x$拿到等号的另一边，可得

$$ F(X) + x = H(x) $$

也就是说，传统神经网络学习的映射关系其实是$F(X) + x$。这种映射在网络构建时可以通过快捷连接（shortcut connection）来实现。在ResNet模型中，快捷连接起着恒等映射的作用。所以它的实现也及其简单——将输入加至输出即可。

残差网络为什么有效

理论上，给神经网络追加层数不应当导致网络退化——例如追加的层均为恒等映射时。但是实际上网络却发生了退化，这意味着求解器在使用多层网络拟合恒等映射也存在着困难。在实际情况中，恒等映射不太可能是最优选择，但是如果最优选择与恒等映射非常接近时，残差网络可以很容易的学习到“恒等映射 + 扰动”这样的分离方案，而非完整的最优映射。

TensorFlow实现

TensorFlow提供了官方实现，地址是

tensorflow/models

Models and examples built with TensorFlow. Contribute to tensorflow/models development by creating an account on GitHub.

GitHubtensorflow

我正在尝试开发一个对新手更加友好的版本，欢迎关注！

yinguobing/models

A playground for friendly deep neural network models. - yinguobing/models

GitHubyinguobing