超越经验风险最小化的mixup
一种极其简单的数据增强方式
封面图片： Pawel Czerwinski
这又是一篇面试时候被问到的概念。深度学习知识范围广，每天都有层出不穷的方法与概念涌现。你永远不会知道下一个问题从何而来。
mixup: BEYOND EMPIRICAL RISK MINIMIZATION是由来自MIT的Hongyi Zhang等人在2018年发表的文章。文中提出了一种改善大规模神经网络过拟合以及对对抗样本敏感的学习方式——mixup。你可以在这里找到原文：
Hongyi Zhang
作者在GitHub开源了相关代码：
hongyi-zhang以下内容为针对该文章的学习笔记。
当前的深度神经网络存在两个共性。第一，它们的训练过程其实是最小化训练数据集平均误差的过程，这个学习规则也被称为经验风险最小化。第二，当下最优的神经网络的参数规模往往与训练样本数量呈现线性关系。然而，学习理论（learning theory）告诉我们，只要学习器的规模不随训练数据数量增长，则经验风险最小化的收敛是确定的。这里的规模是指学习的参数数量，或者VC复杂度。
这种矛盾现象对经验风险最小化用于神经网络训练的合理性构成了挑战。一方面，经验风险最小化使得神经网络即便在强正则化的约束下依旧倾向于记忆训练数据而非基于训练数据泛化。另一方面，经验风险最小化使得神经网络在面对分布与训练数据不同的对抗样本数据时，预测结果会产生极大的偏差。这些证据表明经验风险最小化无法为与训练数据仅存微小差异的测试数据提供解释性与泛化能力。那么是否有替代方案？
使用与训练数据相似而不同的数据实施训练被称为数据增强（data augmentation），它遵循临近风险最小化（Vicinal Risk Minimization）原理。该原理利用人类知识描述与已有训练数据相似的“临近样本”，如此便可以从该相似分布数据中提取额外的训练样本。典型的操作如图像分类时所采用的水平翻转，旋转以及缩放。数据增强可以改善模型泛化性能，但是它与数据本身有关，需要专家知识。另外，数据增强假设临近样本与原始样本的类别相同，无法模拟不同类别样本之间的临近关系。
为解决这个问题，作者提出了mixup——一种简单、不受数据类别影响的数据增强方式。简单的讲，mixup这样构建虚拟训练样本：
$$x ̃=\lambda x_i +(1−λ)x_j \\ y ̃ = λy_i + (1 − λ)y_j $$
其中$x_i, x_j$为输入向量，$y_i, y_j$为独热标签。这里使用的两个样本是从训练数据集中随机抽取的，且$λ \in [0, 1]$。藉由对输入特征的线性差值会导致对应目标的线性插值这一思想，mixup拓展了训练数据的分布。
有监督学习中，我们要寻找的是描述符合联合概率分布$P(X, Y)$的随机特征向量X与随机目标向量Y之间联系的函数$f \in F$。通常会定义损失函数$\ell$作为预测结果$f(x)$与目标$y$之间差异的惩罚项，如$(x, y) \sim P$。之后最小化数据分布P上的损失$\ell$，也被称为期望风险：
$$R(f ) =\int \ell(f (x), y) \text{d} P (x, y)$$
实际情况中分布P是不可知的，可以利用的是满足分布P的数据集合$\mathcal{D}={(x_i, y_i)}_{i=1}^n$。借助该数据集可以得到P的近似分布：
$$P_\delta (x, y)=\frac{1}{n}\sum_{i=1}^n \delta(x=x_i, y=y_i)$$
其中$ \delta(x=x_i, y=y_i)$是$x_i, y_i)$中心的狄拉克质量（Dirac mass）。将预期风险与经验分布$P_\delta$结合即可得到经验风险：
$$R_\delta(f) =\int \ell(f (x), y) \text{d} P_\delta (x, y)=\frac{1}{n}\sum_{i=1}^n \ell(f (x_i), y_i)$$
通过最小化上式来习得$f$即为经验风险最小化。由于经验风险监管下的$f$处理的数据量是有限的n，当$f$的参数数量与n相当时，降低风险的最佳方式无疑是记住该数据集。这无疑是我们不想要的结果（过拟合）。
这种对真实分布P的朴素近似$P_\delta$是众多方法中的一种。在近邻风险最小化中，分布P被近似为：
$$P_\nu (x ̃, y ̃)=\frac{1}{n}\sum_{i=1}^n \nu(x ̃,y ̃|x_i, y_i)$$
其中$\nu$为近邻分布，衡量在训练用特征$(x_i, y_i)$近邻中获得虚拟特征$(x ̃, y ̃)$的概率。一种典型的做法是使用高斯近邻：
$$ \nu(x ̃,y ̃|x_i, y_i)=\mathcal{N}(x ̃-x_i, \sigma^2)\delta(y ̃= y_i)$$
这种方法几乎等效于为训练数据增加加性高斯噪声。使用近邻风险最小化，需要对近邻分布执行采样获得数据集 $\mathcal{D}_\nu: ={(x ̃, y ̃)}_{i=1}^m$，并最小化经验近邻风险：
$$R_\nu(f) =\frac{1}{m} \sum_{i=1}^m\ell(f (x ̃_i), y ̃_i)$$
作者提出了一种名为mixup的通用近邻分布：
$$\mu (x ̃, y ̃|x_i, y_i)=\frac{1}{n}\sum_{j}^n\mathbb{E}_\lambda [\delta ((x ̃=\lambda x_i +(1−λ)x_j,y ̃=\lambda y_i +(1−λ)y_j)]$$
其中的$\lambda \sim \text{Beta}(\alpha, \alpha)$，且$\alpha \in (0, \infty)$。这里的超参数$\alpha$控制插值强度，等于0时即等同为经验风险最小化。
所以mixup究竟是在做什么？作者的解释是：mixup近邻分布可以被认为是一种促使模型f面对训练数据时表现的更加线性的一种数据增强方式。这种线性表现降低模型在面临训练数据以外的数据时不必要的震荡。而且从奥卡姆剃刀原则的角度来看引入简单的线性偏差是一个不错的选择。
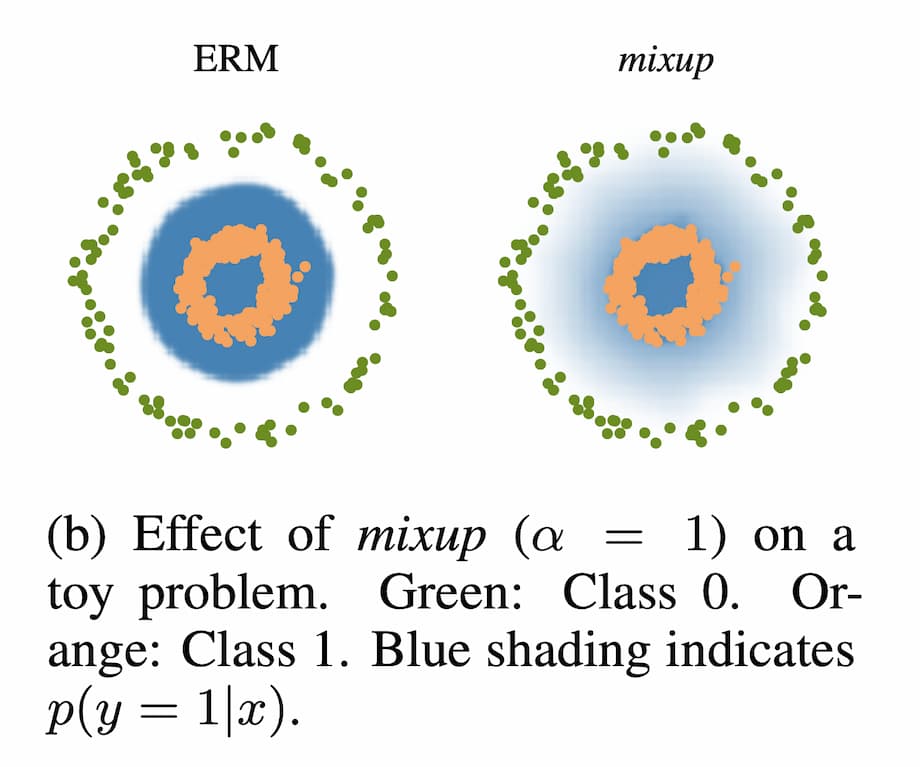
上图展示了一个二元分类问题中，mixup将犀利的决策边界变得平滑。
以上内容基本上解释了mixup的工作原理。原文中还包括大量的实验与分解分析，如果你感兴趣推荐阅读原文，这里不再列出。
另外，原文作者在知乎有回答过相关问题，可以直接向他提问：
张宏毅MIT 机器学习 / 认知科学
Comments ()